线性代数海森矩阵原理和用途详解
一、什么是海森矩阵
海森矩阵(Hessian Matrix),又译作黑塞矩阵、海瑟矩阵、 海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述 了函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家 Ludwig Otto Hesse提出,并以其名字命名。海森矩阵常用于 解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。
具体来说,若一个函数为二次可导的,其Hessian矩阵可以用来描述该函数的局部曲率。Hessian矩阵是一个实对称矩阵,由函数在各变量上的二阶偏导数组成。定义如下:
Hessian=[f_{xy},f_{yx};f_{yx},f_{yy}]
其中,f_{xy} 表示函数对 x 的偏导数和 y 的偏导数的乘积,以此类推。这表明,Hessian矩阵可以刻画函数在某点关于两个变量的共同变化趋势。
梯度是函数对变量的一次偏导数的集合,形成了一个向量。当我们将梯度函数作为变量,它的雅各比矩阵就是该梯度函数的Hessian矩阵。梯度向量 [f_x, f_y] 的雅各比矩阵为:
Jacobian=[f_{xx},f_{xy};f_{yx},f_{yy}]
由此可见,Hessian矩阵实际上就是梯度函数雅各比矩阵的特殊形式。
二. 海森矩阵的由来
海森矩阵(Hessian Matrix)是数学中多元函数
的一种重要工具,用于描述一个函数的二阶导数。其名称来源于德国数学家路德维希·奥托·赫斯(Ludwig Otto Hesse)。海森矩阵能够描述函数的曲率信息,对于优化问题、偏微分方程以及机器学习等领域有着重要的应用。
三. 海森矩阵的原理
海森矩阵是由二阶偏导数组成的矩阵,用于分析多元函数的局部变化情况。给定 ,海森矩阵 为:该矩阵中的每个元素是函数 , 对不同变量的二阶偏导数。海森矩阵在分析局部极值和判断函数凸性方面非常有用。
四、海森矩阵性质
1、对称性:如果函数f在某一区域内二阶连续可导,那么其海森矩阵在该区域内为对称矩阵,即Hi=Hi。
2、特征值与极值点:海森矩阵的特征值在优化问题中具有重要意义。正定性通常指示局部最小值,负定性则指示局部最大值。这一性质使得海森矩阵在判断函数的极值点性质时非常有用。
五、海森矩阵的作用
1、判断多元函数的极值
我们都知道对于一元二阶可导函数,一阶导数为零,二阶导数大于零是极小值点;一阶导数为零,二阶导数小于零是极大值点;一阶导数和二阶导数都为零是驻点。海森矩阵帮助我们把这个理论推广到了多维函数。将海森矩阵进行特征值分解可得如下定理:
矩阵正定(所有特征值为正),该临界点为局部极小值点。
矩阵负定(所有特征值为负),该临界点为局部极大值点。
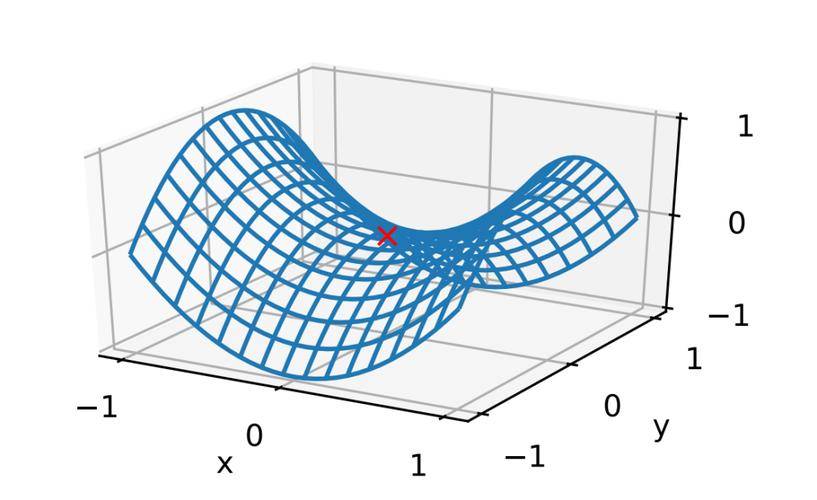
特征值中至少一个为正或者至少一个为负,该临界点为鞍点。
所有非零特征值同号且至少有一个特征值为零,该点无法确定。
2、优化目标函数
我们可以将目标函数在某点的邻域展开成泰勒多项式来逼近原函数。最典型的应用就是牛顿法。牛顿法基于一个二阶泰勒公式展开来近似xo附近的f(x)。
æn+1=æ„-[Hf(æ„)-1▽f(æn),n≥0
其中H代表海森矩阵,如果f是一个正定二次函数,牛顿法能直接跳到函数的最小点。如果不是一个正定二次函数但是在局部能近似为正定二次,牛顿法也可以比梯度下降更快的到达临界点。
五. 海森矩阵的应用范围
- 优化问题:在二次规划或非线性优化问题中,海森矩阵用于加速收敛,通过描述目标函数的局部曲率,帮助判断局部最小值或最大值的存在。
- 机器学习:在深度学习和神经网络的训练过程中,海森矩阵可以用于二阶优化方法(如牛顿法
- ),以改善模型的收敛速度。
- 物理和工程:海森矩阵用于描述多变量系统的稳定性,通过分析系统的二阶导数,可以判断其在某点的稳定性或不稳定性。
具体如下:
1海森矩阵在优化问题中的应用
在最优化问题中,海森矩阵用于判断目标函数的凸性或凹性,从而确定局部极值点是否为全局极值点。 对于一个凸函数,其海森矩阵是半正定的;对于一个凹函数,其海森矩阵是半负定的。 牛顿法是一种高效的数值优化算法,它利用海森矩阵的逆矩阵来计算搜索方向,从而更快地逼近极值点。 然而,对于高维问题,计算和存储海森矩阵的逆矩阵可能非常耗时,因此,拟牛顿法等近似方法被广泛应用,这些方法通过近似海森矩阵或其逆矩阵来降低计算复杂度。
2、海森矩阵在图像处理中的应用
在图像处理中,海森矩阵可以用来检测图像中的特征点,例如角点和边缘。 通过计算图像灰度值的海森矩阵,可以得到图像的曲率信息,从而识别出具有高曲率变化的区域,这些区域通常对应于图像中的特征点。 海森矩阵的特征值可以用来衡量图像的局部曲率,特征值的大小反映了曲率的大小。例如,SIFT(Scale-Invariant Feature Transform)和SURF(Speeded-Up Robust Features)等特征检测算法就利用了海森矩阵来检测图像中的关键点。
3、海森矩阵在机器学习中的应用
在机器学习中,特别是在深度学习中,海森矩阵及其近似方法被广泛应用于优化神经网络模型的参数。 神经网络的训练过程本质上是一个优化问题,目标是找到使损失函数最小化的参数值。 牛顿法及其变种方法,如L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) 算法,利用海森矩阵或其近似来加速优化过程,提高训练效率。 此外,海森矩阵的特征值和特征向量还可以用来分析神经网络的训练动力学,帮助理解模型的泛化能力。
4、海森矩阵的计算与挑战
计算海森矩阵需要计算函数的所有二阶偏导数,对于复杂的函数,这可能是一项非常耗时的任务。 特别是对于高维问题,海森矩阵的规模会非常大,存储和计算其逆矩阵的成本也会很高。 为了克服这些挑战,人们发展了多种近似方法,例如有限差分法和拟牛顿法,这些方法可以有效地近似海森矩阵或其逆矩阵,从而降低计算复杂度。 此外,利用自动微分技术也可以有效地计算海森矩阵,特别是在深度学习框架中,自动微分被广泛应用于计算神经网络的梯度和海森矩阵。
六. 海森矩阵用法及示例
示例 1:计算海森矩阵
对于函数 ,其海森矩阵为:
代码示例:
import numpy as np
from sympy import symbols, hessian
# 定义变量和函数
x, y = symbols('x y')
f = x**2 + x*y + y**2
# 计算海森矩阵
H = hessian(f, (x, y))
H